RRT* 알고리즘을 이용한 경로 계산

1. 개요

  맵-이미지 파일을  갈수 영역(free)을 255(백색), 갈 수 없는 영역(obstacle)을 0(검은색)으로 표현하고, 초기 위치와 목표위치를 설정하고,  RRT* 알고리즘을 이용하여 장애물의 피하면서 갈 수 있는 최단 코스를 계산한다.

 

2. 파이썬 코드

# RRT STAR 알고리즘
import cv2
import numpy as np
import random
import heapq
import os
# image value 255: free area
# image value 0:  obstacle area

class Node:
    """ RRT* 노드를 정의하는 클래스 """
    def __init__(self, point):
        self.point = point
        self.parent = None
        self.cost = 0.0
def draw_path_on_image(img, points, line_color=(0, 255, 0), line_thickness=1):
    for i in range(len(points) - 1):
        cv2.line(img, points[i], points[i+1], line_color, line_thickness)
    return img

def distance(point1, point2):
    """ 두 점 사이의 거리를 계산 """
    return np.linalg.norm(np.array(point1) - np.array(point2))

def nearest_node(nodes, random_point):
    """ 가장 가까운 노드를 찾음 """
    return min(nodes, key=lambda node: distance(node.point, random_point))

def steer(from_node, to_point, extend_length=float('inf')):
    """ 새 노드 방향으로 확장 """
    if distance(from_node.point, to_point) < extend_length:
        return Node(to_point)
    else:
        from_point = np.array(from_node.point)
        to_vec = np.array(to_point) - from_point
        length = np.linalg.norm(to_vec)
        direction = to_vec / length
        new_point = from_point + extend_length * direction
        return Node(tuple(new_point.astype(int)))

def line_collision_check(first_point, second_point, img):
    """ 두 점 사이의 선이 장애물을 피하는지 확인 """
    # 이 부분은 이미지 내부의 장애물과의 충돌을 확인하는 데 사용됩니다.
    # 선분을 구성하는 점들을 생성하고 각 점이 이동 가능한지 확인합니다.
    # 예시로, Bresenham 알고리즘이 이용될 수 있습니다.
    # 여기서는 간단한 방법을 사용합니다.
    x_values = [first_point[0], second_point[0]]
    y_values = [first_point[1], second_point[1]]
    x_values.sort()
    y_values.sort()
    for x in range(x_values[0], x_values[1]+1):
        for y in range(y_values[0], y_values[1]+1):
            if img[y, x] == 0:  # 장애물 검출
                return False
    return True

def choose_parent(new_node, near_nodes, img):
    """ 가장 비용이 낮은 노드를 부모로 선택 """
    if not near_nodes:
        return None
    min_cost = float('inf')
    for node in near_nodes:
        if line_collision_check(node.point, new_node.point, img):
            cost = node.cost + distance(node.point, new_node.point)
            if cost < min_cost:
                min_cost = cost
                new_node.parent = node
                new_node.cost = cost
    return new_node if new_node.parent else None

def rewire(nodes, new_node, near_nodes, img):
    """ 새 노드 추가 후 주변 노드들의 경로 최적화 """
    for node in near_nodes:
        if node != new_node.parent:
            if line_collision_check(node.point, new_node.point, img) and \
                    new_node.cost + distance(new_node.point, node.point) < node.cost:
                node.parent = new_node
                node.cost = new_node.cost + distance(new_node.point, node.point)

def generate_random_point(img, goal, goal_sample_rate):
    """ 목표점 또는 무작위 점 생성 """
    if random.randint(0, 100) > goal_sample_rate:
        return (random.randint(0, img.shape[1]), random.randint(0, img.shape[0]))
    else:
        return goal

def RRT_STAR_search(img, start, goal, iter_max=5000, goal_sample_rate=20):
    """ RRT* 알고리즘 구현 """
    nodes = [Node(start)]
    for i in range(iter_max):
        random_point = generate_random_point(img, goal, goal_sample_rate)
        nearest = nearest_node(nodes, random_point)
        new_node = steer(nearest, random_point, extend_length=30)  # 30은 확장 길이, 조정 가능
        if line_collision_check(nearest.point, new_node.point, img):
            near_nodes = [node for node in nodes if distance(node.point, new_node.point) <= 60]  # 60은 주변 노드 범위, 조정 가능
            new_node = choose_parent(new_node, near_nodes, img)
            if new_node:
                nodes.append(new_node)
                rewire(nodes, new_node, near_nodes, img)
        if distance(new_node.point, goal) <= 30:  # 목표에 가까워진 경우 종료
            return get_path(new_node)

def get_path(node):
    """ 생성된 노드에서 경로 추출 """
    path = []
    while node:
        path.append(node.point)
        node = node.parent
    return path[::-1]  # 경로를 역순으로 반환

if __name__ == '__main__':
    # 이미지 로드 (0: 이동 불가능, 255: 이동 가능)
    #resolution: 20cm
    img = cv2.imread('p20cm_map.png', cv2.IMREAD_GRAYSCALE)
    print('width=',img.shape[1],' height=',img.shape[0])
    # 시작점과 목적지 설정
    # 1000,1000  => 1270, 600
    start_point = (1000, 1000)  # 시작점 좌표
    goal_point = (1270,600)  # 목적지 좌표

    path = RRT_STAR_search(img, start_point, goal_point)
    # 결과 출력
    print("final Path:", path)
    img= draw_path_on_image(img, path, line_color=(0, 255, 0), line_thickness=1)
    cv2.imshow('image', img)
    cv2.waitKey(0)
    cv2.destroyAllWindows()

 

 

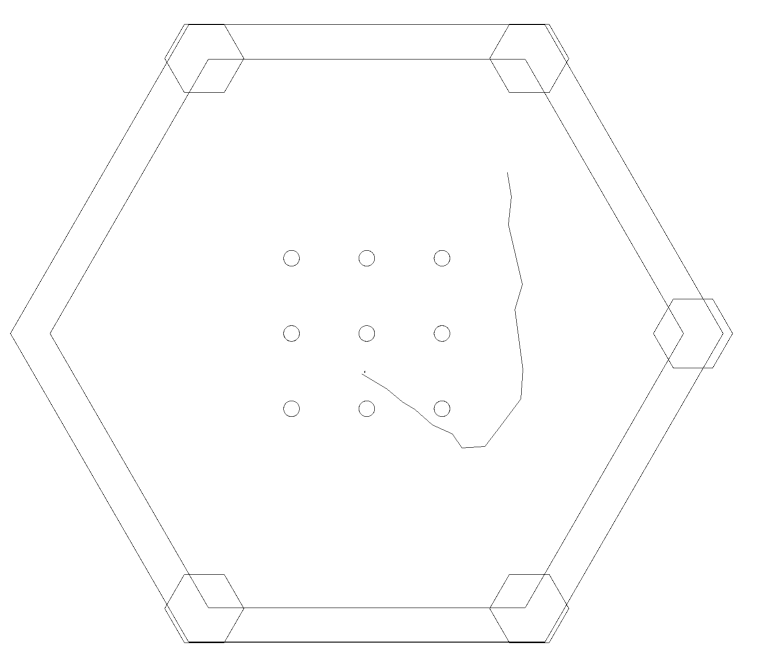
3. 실행결과 예시

    최종결과를 이미지 위에 그려보면 아래와 같은 결과를 얻는다.